V předchozím příspěvku jsem popsal rozdíl v cenách jednotlivých typů bytů v Praze a tvrdil jsem, že jde jen o úvodní analýzu v rámci většího projektu, kterým bylo vytvořit model schopný doporučit cenu bytu na základě jeho vlastností. Z něj by následně bylo možné získat informace o důležitosti jednotlivých parametrů bytu, resp. o jejich vlivu na výslednou cenu.
K tomuto účelu mi posloužil vícenásobný lineární regresní model, který jsem zkonstruoval za pomoci Python knihovny (a stejnojmenného algoritmu) XGBoost. Pokud vás nezajímají jednotlivé kroky při přípravě modelu a jde vám jen o zjištěné závěry, můžete přeskočit rovnou na konec. Pokud vás nezajímají ani zjištěné závěry a hledáte obrázky koťátek, zázračná čínská léčiva nebo poslední recept Ládi Hrušky, asi vám touhle dobou už dochází, že jste tu špatně.
Úprava dat
Po úvodním načtení datasetu popsaného v původním příspěvku bylo potřeba udělat ještě několik drobných úprav. Nejprve bylo třeba vytvořit již dříve zmíněnou proměnnou cena za metr čtvereční a také, stejně jako minule, odstranit z dat byty s celkovou cenou vyšší než 20 mil. Kč, nebo o rozloze větší než 200 m2.
Následně jsem se zbavil sloupců s vlastnostmi bytu, které pro tvorbu modelu nebyly potřeba, nebo je nebylo možné využít. Konkrétně šlo o údaje o zeměpisné šířce a délce bytu, ulici, ve které se byt nachází a jeho celkové ceně. Výsledkem byl dataset s těmito celkem šestnácti proměnnými a jejich hodnotami:
- construction_type (cat) – cihlová / skeletová / panelová / smíšená
- condition (cat) – novostavba / ve výstavbě / projekt / po rekonstrukci / před rekonstrukcí / velmi dobrý / dobrý
- ownership_type (cat)– osobní /družstevní
- floor (cat) – 1st- floor / above_gr / penthouse
- flat_size (int) – velikost bytu v m2
- energy_consumption (cat) – AB / CDEF / G
- dispositions (cat)– 1+1/kk / 2+1/kk / 3+1/kk / 4kk+
- basement (bool) – true / false
- equiped (cat) – ano / částečně /ne
- elevator (bool) – true / false
- accessible (bool) – true / false
- max_floor (cat) – 4- / 5-8 / 9+
- outer_size (cat) – none / small / medium / large / extra large
- parking_space (bool) – true / false
- district (cat) – Praha / Praha 1 / Praha 2 / … / Praha 10
- price_m2 (float) – cena za metr čtvereční bytu
# Import potřebných knihoven
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from IPython.display import display
from sklearn import preprocessing
from sklearn.feature_selection import RFECV
from sklearn.model_selection import KFold, cross_val_score, GridSearchCV
import xgboost as xgb
import time
sns.set_style("darkgrid")
df = pd.read_csv("sreality_dataset_09092019_final.csv", index_col=0, encoding='utf8')
# Vyvtvoření nové proměnné price_m2: cena za metr čtvereční
df["price_m2"] = df["price"]/df["flat_size"]
# Převedení původní proměnné price na hodnotu v milionech CZK
df["price"] = df["price"]/1000000
# Odstranění bytů s cenou přes 20 mil. CZK a velikostí přes 200m2
print("Original dataset size\nNo of columns: %i\nNo of rows: %i\n" % (df.shape[1], df.shape[0]))
df = df[(df["price"] < 20.000001) & (df["flat_size"] < 201)]
print("Dataset size after removal of ads with price over 20 mio. CZK and flat_size over 200 m2\nNo of columns: %i\nNo of rows: %i\n" % (df.shape[1], df.shape[0]))
# Odstranění nepotřebných sloupců lon, lat, street a price
cols_drop = ["lon", "lat", "street", "price"]
df = df.drop(cols_drop, axis=1)
print("List of columns after removal:\n%s\n" % "\n".join(df.columns))
df.head()
Encoding a scaling
V dalším kroku bylo potřeba převést každou kategoriální proměnnou na n-1 binárních proměnných s hodnotami 0 nebo 1 (tzv. encoding), se kterými umí pracovat XGBoost algoritmus. To v překladu znamená, že např. z proměnné „equiped“, která označuje, zda je byt vybaven zcela (hodnota „ano), částečně (hodnota „částečně“) nebo nevybaven (hodnota „ne“), vznikly dvě nové proměnné „equiped_ano“ a „equiped_částečně“, které nabývají vždy jen hodnot 1 nebo 0. Pokud je byt nevybaven, obě mají hodnotu 0.
Takto se počet proměnných rozrostl na rovných 40. Poslední úpravou bylo standardizování kvantitativní proměnné „flat_size“, která označuje velikost bytu v m2.
# Vytvoření listu sloupců pro encoding a následný encoding do n-1 dummy proměnných
cols_enc = [col for col in list(df.columns) if col not in ["flat_size", "price_m2"]]
print("Columns for encoding:\n", cols_enc)
df = pd.get_dummies(df, columns=cols_enc, prefix=cols_enc, drop_first=True)
# Nahrazení mezer v názvech dummy sloupců podtržítky (jinak nefunguje vizualizace stromu přes xgb.plot_tree())
df.columns = df.columns.str.replace(" ", "_")
# Scaling kvantitativní proměnné flat_size
scaler = preprocessing.StandardScaler()
df["flat_size"] = scaler.fit_transform(df[["flat_size"]].to_numpy())
# Vizualizace rozložení hodnot proměnné flat_size po scalingu
fig, ax = plt.subplots()
sns.distplot(df["flat_size"], ax=ax)
ax.set(title="Distplot plot for scaled feature flat_size")
plt.show()
Výběr proměnných (RFECV)
Následující krok obsahoval zkonstruování modelu založeného na všech proměnných, jeho cross-validaci a vyhodnocení jeho přesnosti pomocí předem definované metriky (v tomto případě R2). Vyhodnocení důležitosti jednotlivých proměnných a poté odstranění té nejméně důležité a opakování celého procesu postupně pro všechny kombinace všech proměnných.
Výsledkem tohoto procesu, tzv. RFECV, je potom výběr optimálního počtu proměnných, které by měly vstoupit do finálního modelu. V této fázi byly vyřazeny (jako „nedůležité“) proměnné dispositions_3+1/kk, outer_size_large, district_Praha_6 a jejich celkový počet pro finální model se tím pádem zredukoval na 37.
clf = xgb.XGBRegressor(objective="reg:squarederror")
cv = KFold(n_splits=10, shuffle=True, random_state=42)
selector = RFECV(estimator=clf, cv=cv, step=1, scoring="r2")
# Timestamp začátku, pro měření času běhu
start_time = time.time()
# Výběr features pro model pomocí RFECV (selector.support_ je maska proměnných, které byly vybrány do modelu)
selector.fit(X, y)
print("Original number of features: %i\nOptimal number of features : %d" % (X.shape[1], selector.n_features_))
print("Included features:\n%s" % ", ".join(X.columns[selector.support_]))
print("Removed features:\n%s" % ", ".join(X.columns[~selector.support_]))
# Vizualizace přesnosti modelu (r2) v závislosti na počtu zahrnutých proměnných
fig, ax = plt.subplots(figsize=(6,8))
sns.lineplot(x=range(1, len(selector.grid_scores_)+1), y=selector.grid_scores_, linewidth=3, ax=ax)
# Výpočet rozsahu osy y (dečet horní hranice osy y od spodní) a vzdálenosti nejvyššího bodu grafu od spodní hranice osy kvůli nastavení ymax parametru pro axvline
yaxis_h = ax.get_ylim()[0] - ax.get_ylim()[1]
vline_h = ax.get_ylim()[0] - selector.grid_scores_[selector.n_features_ -1]
# Přidání vertikální čáry v nejvyšším bodě grafu s pomocí parametrů ymax vypočtených výše
ax.axvline(x=selector.n_features_, ymax=vline_h/yaxis_h, color="red", linestyle="--")
ax.set(title="the relationship between the number of features and r2")
ax.set(xlabel="number of features")
ax.set(ylabel="r2")
plt.show()
# Odebrání vyřazených features z datasetu
X = X[X.columns[selector.support_]]
print("--- RFECV took: %s seconds" % (time.time() - start_time))
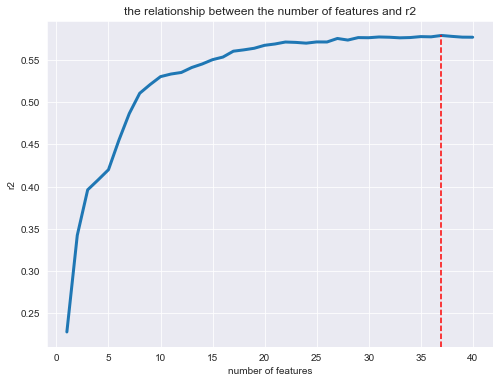
Obrázek dole zobrazuje průměrné hodnoty R2 pro modely, které zahrnovaly různé počty proměnných (od jedné až po všech původních čtyřicet). Červená čára označuje nejvyšší hodnotu, které model dosáhl při zahrnutí všech proměnných s výjimkou tří zmíněných, které byly vyloučeny.
Ladění modelu (GridSearchCV)
Poslední použitou technikou, je takzvaný Grid Search (konkrétní implementace je GridSearchCV), která umožňuje vytvořit velký počet stejných modelů s různými nastaveními tzv. hyperparametrů a následně vybrat ten s nejlepšími výsledky, který je poté využit k predikcím a další práci. Fakt, je, že ačkoliv konkrétně XGBoost má hyperparametrů a různých hodnot, kterých mohou nabývat, přehršel, já jsem jich zkoušel jen relativně velmi málo.
Jeden důvod je, že tato fáze je výpočetně poměrně náročná a může trvat hodně dlouho a druhý a hlavní důvod je, že jsem na hodinách statistiky nedával pozor (což jsem tedy rozhodně měl), takže u spousty parametrů stále ještě tápu, pokud jde o to, co přesně v modelu ovlivňují.
# Timestamp začátku, pro měření času běhu
start_time = time.time()
# Hledání optimálních parametrů pro daný clasifier pomocí GridSearchCV - hlavně max_depth!!!
clf_params = {"max_depth":range(3,7,1),
"learning_rate": [0.05, 0.1, 0.2]}
grid = GridSearchCV(estimator=clf, param_grid=clf_params, cv=cv, scoring="r2")
grid.fit(X, y)
clf_best = grid.best_estimator_
print("Best estimator version is:\n%s" % clf_best)
# KFold cross-validace modelu - získání hodnot R2 a RMSE (nejprve je potřeba převést scores na kladná čísla a poté odmocnit)
r2_scores = cross_val_score(clf_best, X, y, cv=cv, scoring="r2")
mse_scores = cross_val_score(clf_best, X, y, cv=cv, scoring="neg_mean_squared_error")
rmse_scores = np.sqrt(-mse_scores)
print("avg. r2: %f\navg. rmse: %f" % (r2_scores.mean(), rmse_scores.mean()))
# Vizualizace výsledků jednotlivých fází v rámci cross-validace a jejich průměru
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(20,5))
sns.lineplot(x=range(1, len(r2_scores)+1), y=r2_scores, marker="o", markersize=8, linewidth=3, ax=axs[0])
axs[0].axhline(y=r2_scores.mean(), color="red", linestyle="--")
sns.lineplot(x=range(1, len(rmse_scores)+1), y=rmse_scores, marker="o", markersize=8, linewidth=3, ax=axs[1])
axs[1].axhline(y=rmse_scores.mean(), color="red", linestyle="--")
axs[0].set(title="r2 scores of individual folds in CV")
axs[1].set(title="RMSE scores of individual folds in CV")
plt.show()
print("--- GridSearchCV took %s seconds" % (time.time() - start_time))
Predikce a konečně nějaké výsledky
Výsledný natrénovaný model dosáhl hodnoty R2 lehce přes 0,6 (tzn. vysvětlil cca 60 % variability proměnné cena za metr čtvereční). To se na první pohled nemusí zdát moc, ale vzhledem k tomu, kolik faktorů (které jsem buď neměl k dispozici, nebo jsem je do modelu záměrně nezahrnul) vstupuje do procesu určení ceny nemovitosti (např. výhled z bytu, občanská vybavenost v okolí, subjektivní vnímání hodnoty bytu majitelem apod.) to ve skutečnosti není zase tak špatné.
# Vytvoření predikce
y_pred = clf_best.predict(X)
# Porovnání skutečné a předpovězené ceny nemovitosti pomocí KDE plotu, boxplotu a scatterplotu
fig, axs = plt.subplots(nrows=1, ncols=3, figsize=(20,5))
sns.kdeplot(y, label="y", shade=True, ax=axs[0])
sns.kdeplot(y_pred, label="y_pred", shade=True, ax=axs[0])
sns.boxplot(data=[y, y_pred], showfliers=False, ax=axs[1])
sns.regplot(y, y_pred, ax=axs[2])
axs[0].set(title="KDE plots for price_m2 and predicted price_m2")
axs[1].set(title="boxplots for price_m2 and predicted price_m2", xticklabels=["y", "y_pred"])
axs[2].set(title="scatterplot for price_m2 vs predicted price_m2", xlim=(0, axs[2].get_xlim()[1]), ylim=(0, axs[2].get_xlim()[1]))
plt.show()
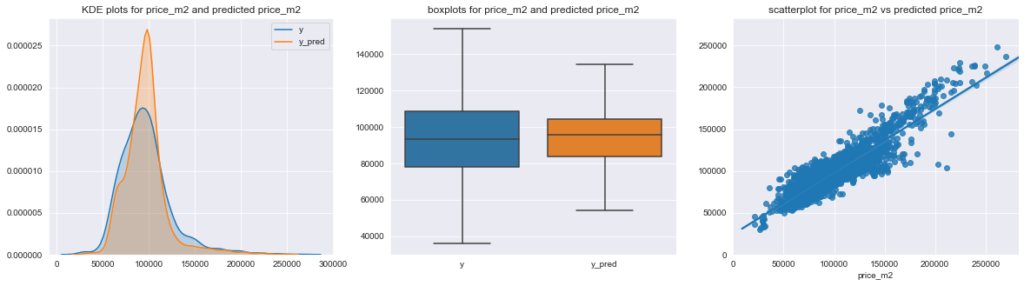
Porovnání predikované a skutečné ceny bytu je popsáno pomocí následujících tří grafů. Z KDE plotu nalevo je vidět, že model častěji bytům přisuzuje „střední hodnotu“ ceny, zatímco reálně je v cenách větší variabilita, než jakou postihuje model (modrá křivka je více „roztažená“, zatímco oranžová je více soustředěná kolem jedné hodnoty). Prakticky to samé vyjadřují i boxploty reálných a predikovaných cen – v realitě je v cenách větší míra variability (která je pravděpodobně daná právě vlivem faktorů, které do modelu nevstupovaly).
To potvrdilo i zpětné zkoumání vstupních dat, kdy se ukázalo, že největší odchylka mezi předpovězenou a skutečnou cenou je u bytů, které mají u informace o ceně nějakou další textovou informaci (např. že o ceně lze jednat, že cena nezahrnuje nějakou podstatnou část bytu apod). Tyto doplňující informace jsem ignoroval, což zpětně nevypadá jako právě šťastné rozhodnutí a stálo by za to je nějakým způsobem zohlednit. Dále se modelu příliš nedaří předpovídat ceny nejdražších bytů. Opět to celkem dává smysl, protože dva byty, které se z hlediska parametrů, které do modelu vstupovaly tváří stejně, budou mít ve skutečnosti odlišnou cenu v závislosti na tom, jestli jeden z nich má zabudovanou výřivku a druhý nikoliv nebo je z jednoho z nich výhled do Stromovky a ze druhého do vnitrobloku, přičemž ani o jedna tato informace by do modelu nevstupovala.
Kvalita modelu
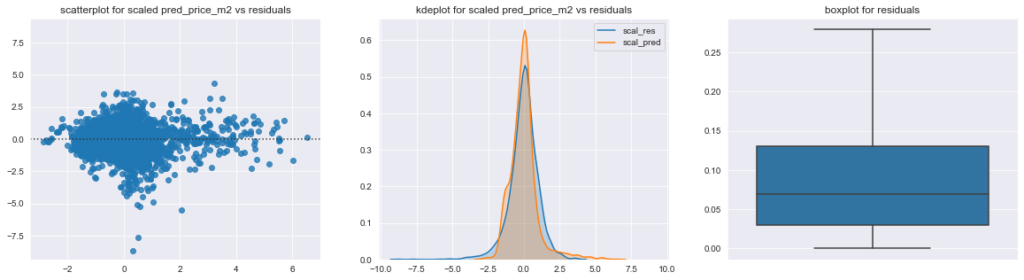
Průměrná chyba modelu (RMSE) je cca 17 tis. Kč za metr čtvereční, což, vztaženo k průměrné ceně bytu v datasetu, která byla téměř 100 tis. Kč, znamená, že v průměru se model s cenou netrefí o asi 17 %. I to vypadá jako relativně vysoké číslo, z boxplotu dole napravo lze ale vyčíst, že pro 25 % bytů, je chyba jen asi 3 %, pro 50 % bytů je to asi 7 % a pro 75 % je chyba menší než 13 %.
Mimochodem, boxplot je zkonstruovaný z procentuální chyby predikce pro konkrétní byty (pokud má byt cenu 100 tis. Kč a model mu předpoví cenu 94 tis. Kč, potom je tato hodnota abs(94-100)/100 = 0,06). Další dva grafy potom ukazují vztah mezi hodnotou reziduí (rozdílem mezi predikcí a skutečnou cenou) a skutečnou cenou bytu (scatterplot vlevo) a také porovnání rozložení jejich standardizovaných hodnot.
# Analýza kvality modelu na základě vizualizace reziduí a predikovaných hodnot
df["pred_price_m2"] = y_pred
df["residuals"] = df["pred_price_m2"] - df["price_m2"]
scaler = preprocessing.StandardScaler()
scal_pred = scaler.fit_transform(df[["pred_price_m2"]].to_numpy())
scal_res = scaler.fit_transform(df[["residuals"]].to_numpy())
fig, axs = plt.subplots(nrows=1, ncols=3, figsize=(20,5))
sns.residplot(x=scal_pred, y=scal_res, ax=axs[0])
sns.kdeplot(scal_res[:,0], label="scal_res", shade=True, ax=axs[1])
sns.kdeplot(scal_pred[:,0], label="scal_pred", shade=True, ax=axs[1])
sns.boxplot(np.abs(df["residuals"])/df["price_m2"], showfliers=False, orient="v", ax=axs[2])
axs[0].set(title="scatterplot for scaled pred_price_m2 vs residuals", ylim=(-max(np.abs(axs[0].get_ylim())), max(np.abs(axs[0].get_ylim()))))
axs[1].set(title="kdeplot for scaled pred_price_m2 vs residuals", xlim=(-max(np.abs(axs[1].get_xlim())), max(np.abs(axs[1].get_xlim()))))
axs[2].set(title="boxplot for residuals")
plt.show()
Důležitost jednotlivých proměnných
Posledním výstupem, který jsem připravil je graf „důležitosti“ (F score) jednotlivých proměnných pro výslednou hodnotu ceny. Tak jak jej stanovil použitý model. Pozitivní je, že na něm není prakticky nic, co by člověka na první pohled překvapilo a do značné míry jen kopíruje závěry, ke kterým jsem došel už v předchozím příspěvku. Zcela zásadní se opět ukázal vliv velikosti bytu, který je s velkým odstupem následovaný dalšími proměnnými.
# Vytvoření df_coefs, který obsahuje proměnné, které vstoupily do modelu a jejich koeficienty
dict_coefs = clf_best.get_booster().get_score()
df_coefs = pd.DataFrame({"feature":list(dict_coefs.keys()), "coef":list(dict_coefs.values()),})
df_coefs.sort_values("coef", ascending=False, inplace=True)
# Vizualizace koeficientu jednotlivých proměnných
fig, ax = plt.subplots(figsize=(10,10))
sns.barplot(x=df_coefs["coef"], y=df_coefs["feature"], color=sns.color_palette()[0], linewidth=0, orient="h", ax=ax)
ax.set(title="importance of individual features", xlabel="f score")
plt.show()
That’s all folks…
Tolik asi k analýze cen bytů v Praze. Pokud jste to dočetli až sem, tak opět nezbývá, než před vámi smeknout klobouk a předem poděkovat za jakýkoliv názor / připomínku / kritiku, kterou budete ochotni mi zanechat v komentářích. S ohledem na to, že celý tenhle projekt jsem dal dohromady za vydatné pomoci Googlu a nezištných hrdinů všedních dní ze Stackoverflow, je asi zřejmé, že jakýkoliv komentář na téma, „co by stálo za to udělat jinak“, „co příště nemá cenu dělat vůbec“, „tohle nedává smysl, lepší by bylo to a to“ apod. pro mě bude mít cenu zlata.